伺服电机控制柜(交流伺服电机矢量控制技术)

关于交流电动机的矢量控制技术，有很多论文和各种文章。但是，它们通常用困难的公式和坐标表示，如果没有扎实的数学和控制理论基础，则很难理解。 Atsushi-kun使用尽可能简单且易于理解的图表和计算来讨论电动机的结构，静态和旋转坐标的变化，矢量控制，伺服控制以及其他电动机驱动技术。

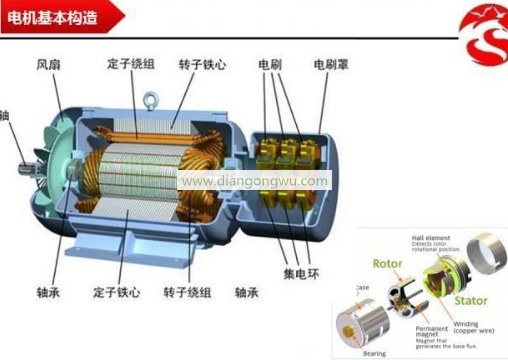
在讨论控制之前，让我们看一下电动机的结构以更好地理解它。实时使用的电机结构非常复杂，但易于理解。电动机由安装在内部的转子和安装在外部的定子组成（也有对置的电动机）。永磁体通常放置在内部。转子和铜线通常缠绕在定子内部。然后将中间轴插入中心以驱动驱动对象。

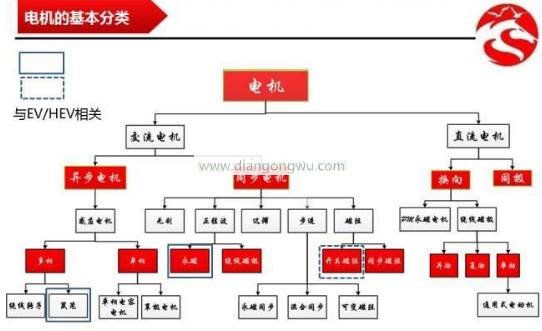
经过100年的发展，电机技术已形成上述各种类别。电机中使用的磁铁是稀土，生产主要分布在中国。由于近年来稀土材料的高价格，业界正在积极研究减少稀土使用，保持性能并降低其性能的方法。产品成本，工程师和企业家，这是一个永恒的话题。同步电动机在当今的实际应用中被广泛使用。

在同步电动机中，安装磁铁的零件主要分为SPM（表面磁铁）和IPM（内部磁铁）。

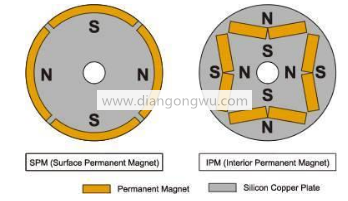
由于控制简单，SPM电动机最初在工业中被采用，但是由于磁体安装在转子表面，因此可用功率主要来自其自身的表面磁体。

IPM电动机可以通过利用磁体和磁体周围的激励力来产生高密度的能量，并且可以通过建筑减少稀土的使用，因此今年将更多地使用它。

SPM电机：

转子（未插入磁体）

定子（线圈缠绕状态）

您会看到定子铁芯上有一个倾斜孔，用于缠绕线圈。倾斜必须能够平均磁场（有关详细信息，请参阅相关论文或专利）。

转子和定子的组合

IPM电机：

转子（未插入磁体）

您可以看到在两个对称位置安装了磁体。这是为了有效地利用激励位置，该中空的对称角影响激励力。如果您有兴趣，可以参考各种专利。 （关于角度问题有许多专利申请）。

定子（线圈缠绕状态）

转子和定子的组合

在下面输入您的主要主题，然后讨论交流电动机控制。

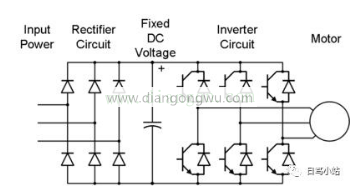
通用电动机驱动变频器如上所述。您会看到IGBT的输出和电动机的输入是三相（电压，电流UVW），电动机的磁体只有S极和N极。同时，三相UVW属于静态坐标，电动机在运行时属于旋转坐标，因此需要根据我们将三相静态坐标交换为两相旋转坐标。目的是要控制电动机。

首先，让我们看一下矢量控制的结构图。

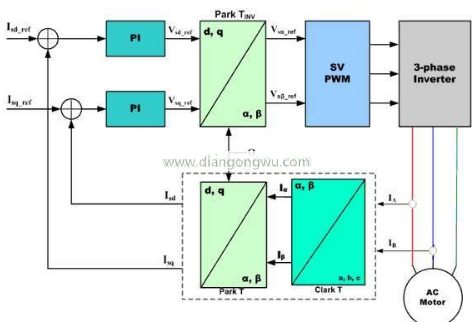
从交流电动机的电流中采样三相交流值，并通过Clark将其转换为两相坐标（αβ），然后通过Park变换将固定的αβ坐标转换为旋转dq坐标，从而形成回馈。计算值和dq命令值。

可以通过PI控制器的计算结果获得dq 2相电压指令值。旋转坐标的dq指令值通过逆Park变换转换为正坐标αβ，然后通过逆Clark变换获得三相电压，并控制SVPWM的输出。

此外，d轴对应于由励磁产生的转矩，而q轴对应于由永磁体产生的转矩。在控制SPM电机时，可以将d轴的指令值设为0。但是，在IPM电机控制中，同时使用了d轴和q轴，因此在速度环中需要两个命令输出。

以下内容计算如何使用正向Clark变换和Park变换执行坐标变换。

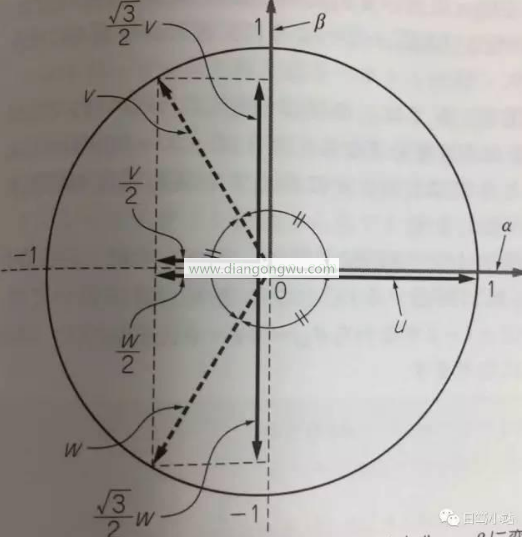
克拉克变换

一致地设置U轴和α轴，并假设k是三相和两相的矢量振幅比系数。从上图可以得到：

α=k {U-1/2V-1/2W}

β=k {sqrt（3）/2V-sqrt（3）/2W}

三级平衡提供了以下好处：

U + V + W=0

α=U

通过上面的公式，我们得到: k=2/3。

所以β=1/sqrt（3）*（V-W）=1/sqrt（3）*（U + 2V）

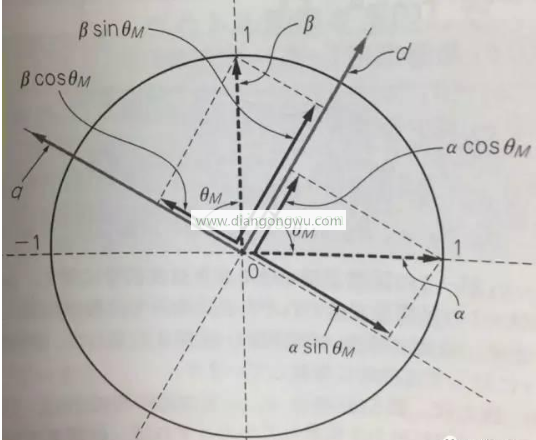
公园改造

假设αβ轴与dq轴之间的角度为θ，我们将αβ分解为dq轴，然后使用三角公式得出：

d=αcosθ+βsinθ

q=-αsinθ+βcosθ

由于旋转坐标和正坐标的逆变换与上述相同，因此在此省略。

我在上面解释了坐标变换和矢量控制结构，矢量控制的目的是在保持电流和电压相位的同时控制伺服，以提高功率效率和电机转矩的效率。让我们看一下包括矢量控制在内的伺服控制结构。

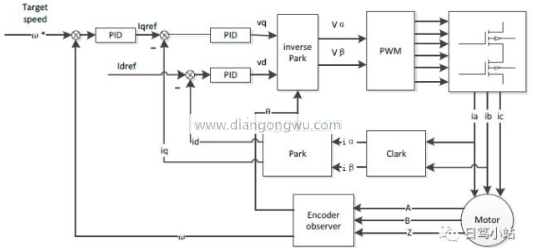
上述结构可以简化为位置控制环，速度控制环和矢量（电流）控制环。

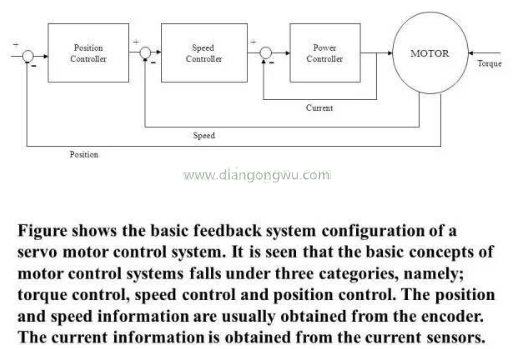
交流电动机的矢量控制分析。在实际的使用变频器的交流电机控制中，由于外部干扰，温度，高频等因素的影响，电机控制算法变得越来越复杂，精度也越来越高，但是如果您已经学会了最基本的方法上面提到的，它将帮助您理解其他将开发的算法。