伺服电机厂家(交流伺服电机的矢量控制)

1.交流感应伺服电机的矢量控制

矢量控制理论是由德国学者F.Blachke于1971年首次提出的。在伺服系统中，直流伺服电动机可以实现出色的动静态性能，其根本原因是仅控制电动机磁通Ф和电枢电流Ia，并且这两个量是独立的。而且，电磁转矩（Tm=KTФIa）与磁通Ф和电枢电流Ia成正比。因此控制简单，性能线性。如果能够模拟直流电动机，则可以单独且独立地获得和控制与交流电动机相对应的磁场和电枢电流，并且交流电动机将具有与直流电动机相似的优异特性。因此，需要将三相交叉变量（矢量）转换为等效的直流量（标量），设置交流电动机的等效模型，然后使用直流电动机的控制方法进行控制。

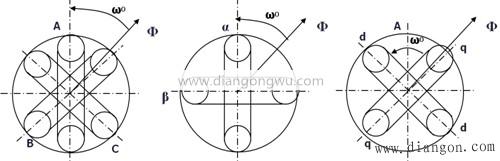
下图所示的三相异步交流电动机在空间中产生角速度为ω0的旋转磁场Φ。在图b中，使用了两组绕组的相距为900的α和β，并且使用了两相之间时间差为900的两个交流电来产生旋转磁场Φ，该旋转磁场的角速度等于ω0，则该图可以认为是a。它与图b中的两组绕组相同。在图c的模型中，当两个彼此垂直的绕组d和q分别通过直流电流id和iq时，会产生一个固定位置的磁场Φ，而当绕组以角速度ω0旋转时，设定的磁场磁场还绘制了旋转磁场的幅度和速度。

将3相A，B和C系统转换为2相α，β系统

此转换是将3相AC电动机转换为等效2相AC电动机。上图a所示的三相异步电动机的定子三相绕组彼此间隔了1200个空间角，当三相平衡交流电流iA，iB，iC通过时，磁场矢量Φ旋转。在定子中产生同步角速度ω0。三相绕组的功能可以由两个在空间上彼此垂直的固定α和β绕组代替，并且使用时差为900的两相交流电iα和iβ来产生旋转磁。所产生的场振幅和角速度也分别为Φ和ω0，在上面的图a和b中，两组绕组可以认为是相等的。

应用三相/2相数学转换公式，将其转换为两相交流绕组的等效交流磁场。产生的空间旋转磁场与三相A，B和C绕组产生的旋转磁场一致。将三相绕组的A相绕组的轴与α坐标轴对齐，磁势为

可以根据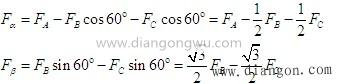磁势与电流之间的比例关系获得对应的电流值iα和iβ。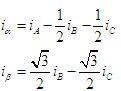三相交流电势转换除磁势转换外，用于转换的其他物理量与三相平衡和两相平衡相同时相同。这样，将三相电动机转换为两相电动机。

矢量旋转变换

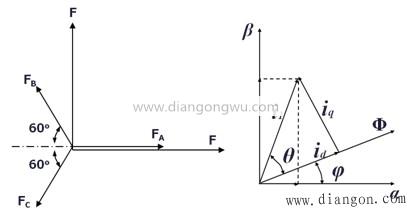
将三相电动机转换为两相电动机后，需要将两相交流电动机转换为等效的直流电动机。如果d为励磁绕组，则传输励磁id，q为电枢绕组，并传输电枢电流iq，从而在定子中产生一个固定振幅磁场Φ，该磁场以角速度ω0旋转。这样，它可以看作是直流电动机。将两相AC电动机转换为DC电动机基本上是矢量到标量的转换，这是从固定的笛卡尔坐标系到旋转笛卡尔坐标系的转换。在这里，将iα和iβ转换为id和iq，转换条件是确保合成磁场不变。 iα和iβ的所得向量为i1。在垂直于Φ方向的方向上投影以获得id和iq。 id和iq在空间中以角速度ω0旋转。转换公式如下：

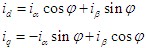直角坐标和极坐标转换

在矢量控制中，还使用了直角坐标和极坐标系转换。在id和iq中找到i1。公式为：

与同等的直流电动机相比，使用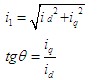矢量转换的感应电动机具有与直流电动机相同的控制特性，其结构简单可靠，电动机容量不受限制，并且机械惯性较小。

使用矢量转换的感应电动机具有与直流电动机相同的控制特性，结构简单可靠，电动机容量不受限制，并且机械惯性小于等效直流电动机。

2. 交流同步电机的矢量控制

基本原则

在直流电动机中，无论转子在哪里，由转子电流产生的电枢磁力始终与定子磁极产生的磁场保持90°的电角度。因此，转矩仅与电枢电流成正比。交流永磁同步电动机的定子具有三相绕组，转子是由永磁体构成的磁极。转子位置编码器同轴连接，以检测转子磁极与定子绕组的相对位置。该位置与转子角的正弦函数有关。位置编码器与电子电路相结合，使得在三相绕组中流动的电流与转子位置角之间的正弦关系为120°。由三相电流合成的旋转磁力始终相对于空间中的转子磁场保持90°（线性）的电角度以产生最大转矩。可以设置永磁磁场，电枢磁力和转矩，并在调速过程中使用控制电流来达到转矩控制，矢量控制的目的。